用二次諧波色散掃描表征超短激光脈沖

（本文譯自Characterizing ultrashort laser pulses with second harmonic dISPersion scans，Ivan Sytcevich, Chen Guo, Sara Mikaelsson, Jan Vogelsang, Anne-Lise Viotti, Benjamín Alonso, Rosa Romero, Paulo T. Guerreiro, Anne L’Huillier, Helder Crespo, Miguel Miranda, and Cord L. Arnold）

1. 介紹
超短激光脈沖已成為眾多科學和工程領域不可或缺的工具，在物理、化學、材料加工和醫學等領域都有廣泛的應用。幾乎就在激光發明之后，被動鎖模技術的引入產生了持續時間在皮秒-秒范圍內的光脈沖[1,2]。Ti:Sapphire作為激光活性材料的發現是在八十年代中期[3]，以及啁啾脈沖放大(CPA)[4]和克爾透鏡鎖模[5]導致了該技術的快速商業化和傳播。非線性后壓縮技術[6-8]為可見光和近紅外光譜區域的脈沖提供了低至幾fs的脈沖。在這種情況下，脈沖包絡線只包含少量的電場振蕩，從而產生各種令人興奮的物理現象[9,10]。這種超短脈沖可以通過高階處理產生更短的波形諧波產生[11,12]，它進一步將可實現的脈沖寬度降低到阿秒范圍[13-15]，使實驗研究具有前所未有的時間分辨率。

超短激光脈沖的許多應用需要精確的表征，即確定激光脈沖的精確波形或至少確定其脈沖強度分布。兩者都是具有挑戰性的任務，因為在時域內直接訪問脈沖信息并不容易。直接的時間分辨診斷，例如條紋測量[16]和基于電光采樣的方法[17]已經得到證實。

然而，這些技術需要強大的激光脈沖和復雜的設置。人們提出了一些要求較低的實驗方法來表征超短脈沖。強度自相關測量是z早被引入的技術之一[18]，目前仍被廣泛使用。它記錄非線性信號(通常是二次諧波)的強度作為兩個脈沖副本之間延遲的函數，以獲得脈沖時間剖面持續時間的估計。然而，準確的脈沖幅度和相位信息仍然無法獲得[19]。通過在檢測方案中加入一個光譜儀，測量每個延遲的頻譜，可以得到二維頻譜圖，這是頻率分辨光學快門FROG技術的基礎[20,21]。利用迭代數學算法，相位和幅值都可以被恢復，脈沖完全重構。另一種流行的方法，稱為直接光譜相位干涉法電場重建(SPIDER)[22,23]依賴于記錄兩個延遲和頻率剪切脈沖副本之間的頻譜干擾模式。相較而言，這種方法不需要復雜的反演算法，但需要更復雜的光學設置。

另一類表征技術不依賴于脈沖副本，而是在譜域中操縱脈沖。在多光子脈沖內干涉相位掃描(MIIPS)是一種頻譜相位整形器，用于在測量二次諧波頻譜時對脈沖施加受控相位函數[24]。群延遲色散(GDD)曲線可以通過確定哪個函數局部抵消原始頻譜相位從而使二次諧波產生z大化而得到(SHG)輸出，從而允許反演光譜相位，進而重建時間脈沖輪廓。除了MIIPS外，也報道了利用脈沖整形器的相關方法[25,26]。

色散掃描，簡稱d-scan，利用了一個與MIIPS密切相關的概念(27、28)。通過引入可變色散元件，例如玻璃楔對或棱鏡/光柵壓縮器，將光譜相位應用于要表征的脈沖。通過改變色散的量，例如，通過在光束內外移動變厚度的玻璃楔，并記錄非線性信號的頻譜(例如，二次諧波)，產生二維跡線，可以通過迭代算法根據與FROG反演類似的策略獲得相位信息。d-scan技術的直接優勢是設置簡單，不需要脈沖復制或光譜剪切。此外，d-scan通常使用壓縮器來操縱光譜相位，這是幾乎任何超快激光器的基本組成部分，因此可以同時壓縮和表征超短光脈沖。自發明以來，d-scan已成為各地許多實驗室公認的技術。它已經在不同的目標脈沖寬度和中心頻率下實現和測試，d-scan壓縮脈沖已經實現了從泵浦探測光譜到生物醫學成像的各種應用[29,30]。

在本文中，我們簡要介紹了d-scan技術的主要特點，并概述了隆德激光中心 (LLC)zui近的發展和取得的成果。在第2節中，我們提供了一個基本的理論描述，并介紹了描述d-scan測量所需的數學框架。我們給出了如何解釋d-scan軌跡和如何選擇相位恢復策略的見解。在第3節中，我們描述了該技術用于不同波段和脈寬的測量的不同實驗實現。接下來，我們提出單發方法，并討論使用d-scan作為單發技術的優點和局限性(第4節)。zui后，對該方法的發展進行了總結和展望。

2. 理論
2.1. d-scan測量的概念
我們首先提供了一個簡單的理論描述，并討論了d-scan測量的一般性質。這將進一步幫助理解這種表征技術的優點和局限性，以及某些工程解決方案背后的原因。

代表激光脈沖的復電場在頻域中可以表示為:

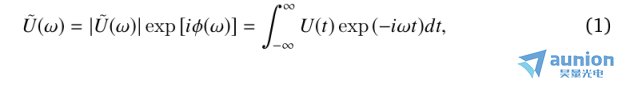
式中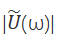為譜幅，φ(ω)為譜相位，U(t)為時域響應復電場。脈沖在厚度為z的透明介質中傳播相當于將式(1)與相位項相乘:

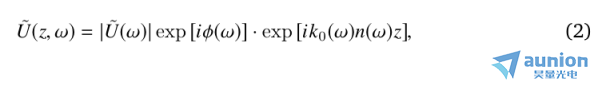
其中n為介質的折射率，k0為真空波數。

脈沖測量技術通常采用非線性過程來獲得脈沖幅度和相位靈敏度。在數學上，非線性相互作用的結果可以寫成

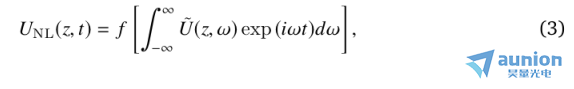
其中f表示特定的非線性相互作用。在本文中，我們主要處理二次諧波產生(SHG) d-scan，其中f簡單地表示平方。zui后，測量該過程的功率譜作為色散的函數，得到二維跡線：

上面給出的簡單模型假設基波輻射與非線性信號的理想耦合，這意味著在脈沖帶寬上有完美的相位匹配。對于寬帶少周期脈沖，通常不是這樣[31,32]，必須包含響應函數R(ω)(可能不僅包含有限相位匹配的影響，還包含技術參數，例如光譜儀響應函數)以適應不規則的光譜響應。

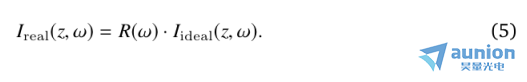
圖1(a)給出了中心波長為800 nm的理想10 fs-FWHM(z大半高全寬)高斯脈沖的二次諧波d-scan跡線。在這個模擬中，根據塞米爾方程計算了BK7玻璃的折射率，BK7玻璃是可見光和近紅外光譜范圍內d-scan玻璃楔的常用材料。在圖1(b-d)中，我們在譜相位的泰勒展開中加入數值上不同的色散階數，即群延遲色散(GDD)、三階相位色散(TOD)和四階相位色散(FOD)。對脈沖施加正GDD主要是沿著色散軸向下移動走線(圖1(b))，這意味著可以通過移除玻璃來重新壓縮脈沖。由于BK7不僅引入GDD，還引入了高階項，因此軌跡似乎略有傾斜。這在圖1(c)中變得很明顯，圖中顯示了帶有TOD的d-scan跡線，導致跡線相對于色散軸幾乎呈線性傾斜。zui后，FOD導致拋物線狀變形(圖1(d))。這些簡單的例子突出了d-scan測量對脈沖光譜相位的靈敏度。因此，d-scan軌跡提供了一種直觀的方法來直觀地估計壓縮脈沖的質量，即使不使用重建算法，這是一種非常有用的日常優化指標，例如來自空芯光纖(HCF)壓縮器的少周期脈沖[33,34]。

 

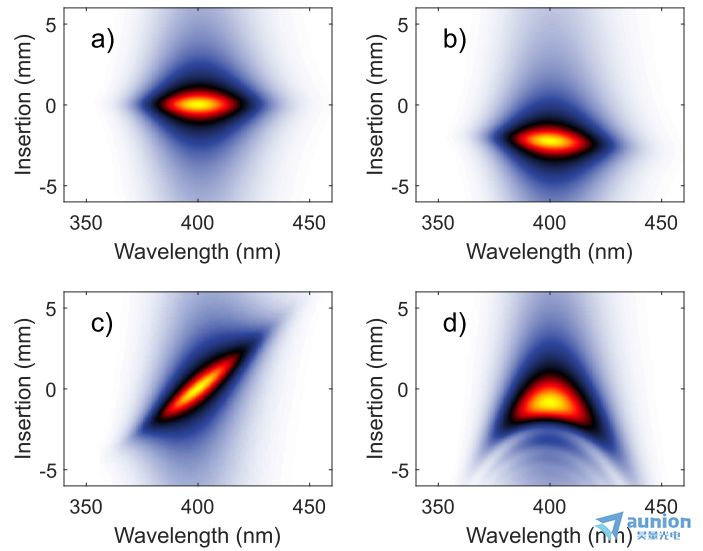
圖1所示，在不加相位的情況下，以800 nm為中心的10 fs高斯脈沖的模擬二次諧波 d-scan跡線(a)，100 fs2 GDD (b)，800 fs3 TOD(c)，8000 fs4 FOD (d)。

2.2. 相位反演

計算一個已知脈沖的d-scan軌跡是一個比較簡單的程序。然而，反過來，即從測量的d-scan軌跡中提取信息，并不是一項微不足道的任務。在數學上，這屬于逆問題的范疇，并由稱為相位反演算法的數學程序來解決。主要的想法是找到產生與實驗數據幾乎相同的軌跡的脈沖。在數值上，我們尋求z小化實驗測量和計算軌跡之間的均方根誤差G，以m = 1,2，…Nm不同頻率點，k = 1,2，…Nk不同的玻璃插入來采樣:

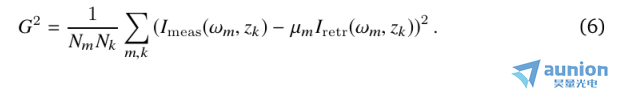
在這里，Imeas和Iretr分別是測量和模擬的跡線，和

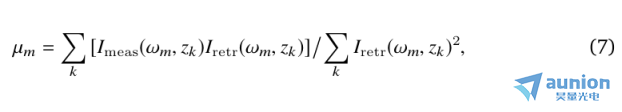
是在每次迭代中計算和更新的z小化因子。為了成功反演，µm給出譜響應函數R(ω) [Eq.(5)]。由式6可知，使Gz小化的脈沖反演本質上是一個非線性zui小二乘問題。

解決這類問題是一個被廣泛研究的數學領域。zui小二乘解Nelder-Mead (NM)， Levenberg-Marquardt (LM)或Broyden-Fletcher-Goldfarb-Shanno算法可以很容易地實現為脈沖反演工具，并廣泛用于d-scan。NM算法或下山單純形方法，一種在早期d-scan工作中主要使用的方法[27,28]，被證明是魯棒和可靠的，盡管速度較慢。據報道，在自校準d-scan技術中使用了基于LM算法的z小化，其中壓縮器參數，即引入的色散，

也可以從測量中反演[35]。這反過來又可以量化和消除超連續光纖激光器中的脈沖序列不穩定性[36]。另一個例子是基于差分進化的d-scan反演算法[37]，與NM相比，該算法除了收斂速度更快外，還不容易在局部ji小值處停滯。一般來說，為了有效地使用這類算法，選擇方便的譜相位參數化是有益的。展開成傅里葉級數通常會提高收斂速度，但在某些情況下也有陷入局部ji小值的風險。一個可能的解決這個問題的方法是使用樣條插值代替[38]，或者在停滯發生時切換到不同的基礎[27]。長期以來,“干凈”脈沖，通常有簡單的d-scan跡線，相位的泰勒級數表示也可以使用。

另一類檢索算法，通常主要與FROG一起使用，是基于迭代約束的反演算法(例如廣義投影或基于ptychoography的方法)，其靈感來自衍射成像的早期工作[39]。這種方法的主要特點是在反演脈沖上引入一組特定的約束，使誤差G (eq. 6)在每次迭代中減小。相比于前面提到的“蠻力”z小化，這可以說是解決相位反演問題的更優雅的方法[40,41]。然而，這種加速往往是以魯棒性降低為代價的，特別是在處理被噪聲污染的跡線時。這zui近歸因于這樣一個事實，即這些算法在存在高斯噪聲時不會收斂到z小二乘解[42]。因此，z好選擇在這些條件下更可靠的一般zui小二乘解[43]。舉個例子，zui近提出了一種基于數據(或強度)約束的d-scan相位反演算法[44]。在這里，數據約束意味著模擬的復雜d-scan軌跡的振幅被測量數據取代，而相位信息在算法的每次迭代中都保持不變。與NM方法相比，該方法具有更快的收斂速度，但同時明顯更容易受到噪聲的影響[44]。

一般來說，設計快速，魯棒和高效的反演算法是一個活躍的研究領域，并且大量的努力致力于開發針對脈沖表征問題進行優化的程序。例如，zui近提出的通用脈沖反演算法(COmmon Pulse Retrieval Algorithm, COPRA)[42]是一種通用算法，不僅適用于d-scan，還適用于其他幾種方法，如FROG或MIIPS。雖然受到基于約束的方法的啟發，但COPRA通過在算法運行的zui后階段用梯度下降取代數據約束步驟，巧妙地避免了前面提到的無法達到z小二乘解的問題。這反過來又有助于提高具有高高斯噪聲水平的跡線反演的準確性。另一個令人興奮的發展是使用人工神經網絡進行脈沖重建[45]，zui近也報道了d-scan[46]，顯示了令人印象深刻的毫秒級反演時間，從而打開了與單次d-scan系統相結合的“實時視圖”脈沖監測的可能性。

3. 實現
d-scan技術于2012年首次演示[27]，當時主要集中在近紅外的少周期光源脈沖的表征上，此后人們一直在努力擴展其對不同持續時間和中心頻率脈沖的適用性，將各種非線性現象與不同的方法相結合，以引入所需的色散變化。

由于非線性介質的可用性和高信噪比(SNR)，例如與三階過程相比，在d-scan測量中非線性相互作用z受歡迎的選擇是SHG。然而，在某些情況下，SHG的使用限制了d-scan的適用性。普通SHG晶體的相位匹配帶寬有限，通常會降低單發d-scan裝置的有效光譜范圍。zui近報道了一種可能的解決方案：使用介電納米粒子作為非線性介質，它不受相位匹配的限制[47]。另一個問題發生在測量具有倍頻程光譜的脈沖時，其中在基頻和二次諧波場的某些頻率成分之間存在重疊。在這種情況下，必須仔細過濾有用信號，例如使用空間掩模或偏振器[48]。不過，值得一提的是，這種通常不受歡迎的特征可能是有益的：基頻和二次諧波場產生的干擾對載波到包絡相位很敏感，在反演算法中包含這一信息可以完全重建電場波形[49]。

高階非線性過程，例如三次諧波產生(THG)，可以用來緩解這些問題。基于THG在石墨烯[50]和TiO2−SiO2化合物薄膜[51]中的d-scan裝置已經有報道。這些材料具有較大的非線性系數，從而減少了三階相互作用效率低的問題。對于光譜含量向紫外方向延伸的脈沖，由于需要專門的深紫外光譜儀，基于頻率上轉換的方法很快變得不切實際。另一個問題是缺乏合適的非線性晶體在UV中進行有效的頻率轉換，因為該區域的強色散阻止了寬相位匹配，并且在大多數材料中，吸收變得很重要。為了解決這一問題，引入了基于退化非線性過程的方案，其中非線性信號的頻率與驅動場相同。其中一種方案是交叉極化波生成(XPW)，該方案已成功應用于d-scan，用于表征近紅外[52]和深紫外[53]的脈沖。在XPW中，要檢測出信噪比好的信號，關鍵是驅動場具有高度的線偏振和XPW后消光比大的偏振方案。d-scan測量中使用的另一種簡并過程是自衍射[54]，它可以同時測量兩個未知的近紫外脈沖[54]。

即使在一個選定的非線性相互作用的情況下，d-scan的實驗實現仍然可以根據中心頻率和脈沖持續時間(頻譜帶寬)有很大的不同，如圖2所示。一般來說，光源的變換限制脈沖持續時間越長(譜帶寬度越小)，色散掃描窗口就應該越大，以便捕捉到z佳壓縮點周圍二次諧波的演變。對于非常短的脈沖，即使少量的GDD應用也會導致顯著的壓縮/加寬，而對于達到ps寬度的長脈沖或具有大時間帶寬積的脈沖，所需的GDD窗口可以高達數十萬fs2。對于GDD窗口而言，究竟應該掃描多少色散才能獲得穩健的測量和反演，這不是一個簡單的問題，需要嚴格的數學研究，這超出了本文的范圍。在這里，我們的目標是根據我們在測量不同激光系統脈沖時的經驗給出實用值。

 

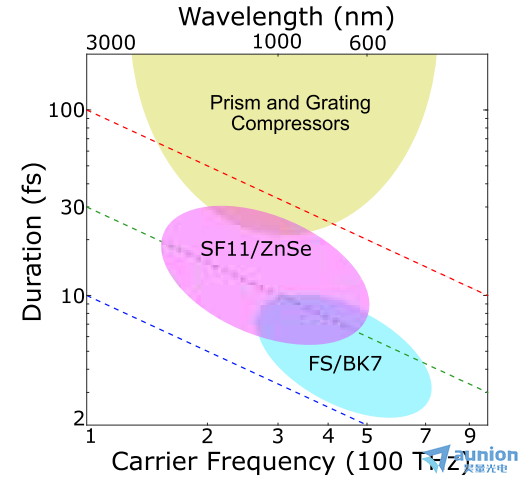
圖2所示。作為目標脈沖頻率和中心頻率函數的SHG d-scan實現。藍色、綠色和紅色虛線分別對應于給定頻率下1、3和10個光周期的持續時間。陰影區域表示不同的光學元件，它們可以作為d-scan測量中的掃描色散元件。淺藍色和粉色區域對應于使用指定材料的玻璃楔對配置。

早期的設計，使用由熔融石英或BK7玻璃制成的楔形，GDD在30-50 fs2/mm范圍內，非常適合測量由空芯光纖(HCF)壓縮器或基于光學參數啁啾脈沖放大(OPCPA)的激光器發射的可見和近紅外(NIR)中心頻率的短周期脈沖[27,55,56](圖2中的淺藍色陰影區域)。圖3給出了一個典型的二次諧波d-scan裝置。在通過啁啾鏡像對后，脈沖通常是負啁啾的。通過微調玻璃楔的插入，從而引入正GDD，可以控制啁啾，并且補償來自光束路徑進一步向下的光學元件對實驗的貢獻。一個薄的SHG晶體，一個濾波器(抑制基波輻射)和一個光譜儀是執行測量所需的唯yi額外組件，使這種配置可以直接實施。此外，由于在任何點都沒有光束分裂和重組，因此記錄具有良好信噪比的跡線所需的脈沖能量非常低，允許直接從振蕩器測量脈沖。在放大脈沖的情況下，可以通過僅使用主脈沖能量的一小部分(例如玻璃板/楔形反射)寄生測量。

 

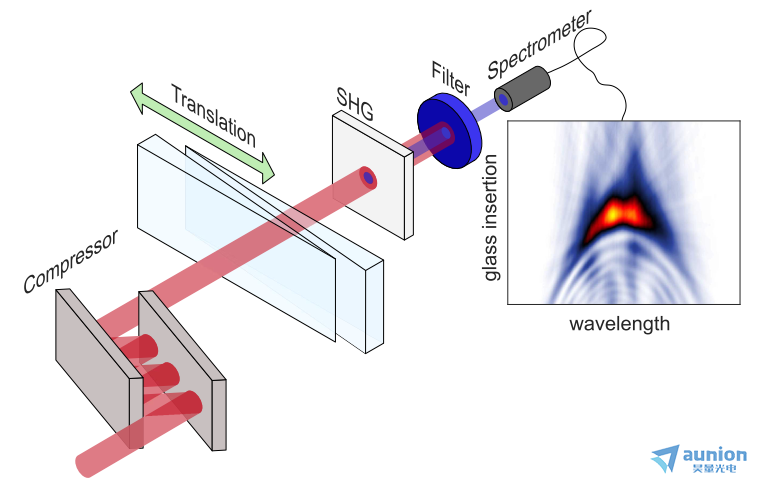
圖3所示。基于SHG的d-scan裝置用于表征少周期脈沖。光通過由啁啾鏡和玻璃楔對組成的壓縮器;引入的GDD通過其中一個玻璃楔子的運動進行微調。用光譜儀對薄晶體中產生的二次諧波信號進行檢測，并在不同的楔形位置記錄譜圖，得到譜圖。

圖4(a)所示為位于LLC的低周期高重復率Ti:Sapphire種子OPCPA激光器[57]的輸出記錄的d-scan軌跡。使用一對BK7玻璃楔(在800 nm處的群速度色散(GVD)約為45 fs2/mm)作為色散元件，色散窗口僅為180 fs2就足以進行掃描。二次諧波是在薄BBO晶體中產生的。基波輻射用偏振器過濾，信號用光纖耦合光譜儀記錄。從反演到的跡線中提取脈沖信息(圖4(d))得到的FWHM持續時間為5.8 fs(圖4(g))。

當處理中心波長更遠的紅外脈沖時，使用由普通光學玻璃制成的楔子來引入足夠的色散變化通常是具有挑戰和不切實際的。使用密度更大的材料，例如SF10-SF57燧石，ZnS, ZnSe等，它們具有更大的總體色散和零色散交叉，進一步到紅外(與標準玻璃相比)，標準d-scan裝置的工作范圍可以擴展到更長的脈沖(約20 fs)和波長范圍(<1.5µm，如圖2中粉紅色表示)。

 

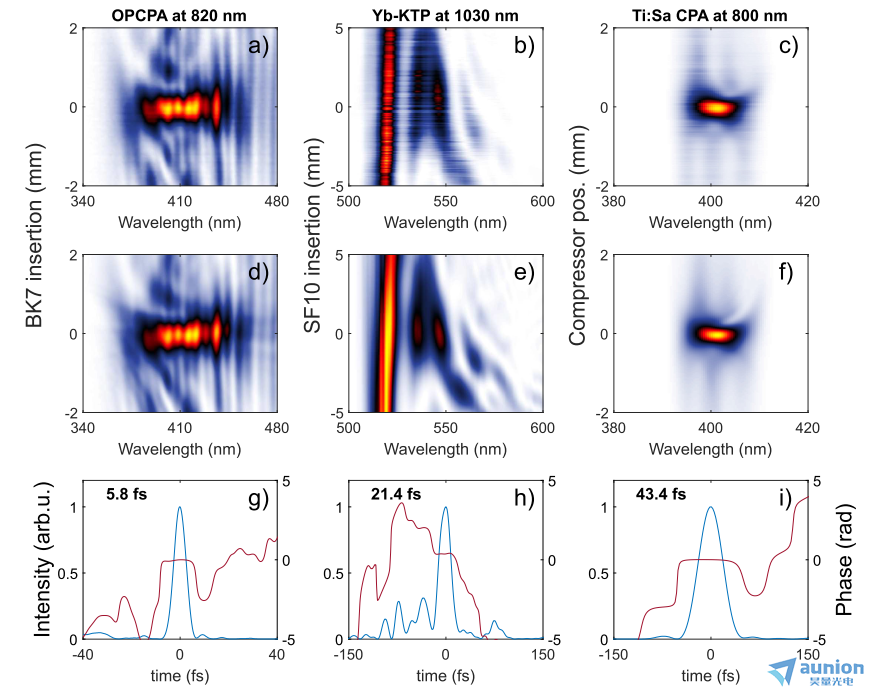
圖4所示。不同脈沖持續時間下的SHG - d-scan：(a)-(c)：分別使用來自幾個周期OPCPA系統、經過KTP晶體后壓縮的Yb激光器[58]和來自10 Hz CPA激光系統的脈沖的平均測量軌跡；(d)-(f)對應的反演軌跡；(g)-(i)反演到的脈沖強度分布圖和相位。

圖4(b)顯示了單疇磷酸鈦基鉀晶體(KTiOPO4或KTP)中具有非線性后壓縮階段的固態Yb激光器(中心波長1030 nm)脈沖的測量d-scan跡線[58]。在此測量中，d-scan裝置幾乎與圖3所示的設置相同，唯yi的區別是使用SF10玻璃楔，在1100 nm(壓縮脈沖的中心波長，色散窗口為920 fs2)引入約92 fs2/mm的GVD，而BK7在該波長僅為19 fs2/mm。反演到的跡線(圖4(e))顯示了21.4 fs長的脈沖，在強度分布中有一系列預脈沖，來自未補償的三階色散。

對于更長的多周期脈沖(>25 fs)，使用棱鏡或光柵壓縮器會引入適量的色散(圖2中的黃色區域)。壓縮器是放大的短脈沖激光器的組成部分，可以方便地用于執行d-scan。圖4(c)給出了使用光柵壓縮器作為色散元件的d-scan測量。結果是用Ti:Sapphire TW級激光器獲得的，工作頻率為10 Hz，在LLC驅動高強度阿秒脈沖光束線。壓縮器中的一個光柵安裝在一個電動平移臺上，該平臺在z佳壓縮點上連續移動。壓縮器的分散系數為4300fs2/mm GVD。總掃描色散窗為17200 fs2，反演脈沖持續時間為43.4 fs。

4. 單發d-scan
到目前為止，我們已經討論了通過在脈沖壓縮器內機械移動光學元件來施加色散變化的d-scan實現。對于具有高重復率(> 1 kHz)和脈沖對脈沖穩定性的激光系統，這不會影響脈沖表征的準確性。得到的d-scan軌跡允許在脈沖序列中反演平均脈沖。然而，對于低重復率的激光裝置或表現出脈沖持續時間波動(這在TW - PW級超高強度系統中相當常見)，上一節提到的解決方案可能不實用，需要很長時間才能完成，或者在脈沖不穩定的情況下根本不準確。

單發FROG在推出后不久就出現了[59]，而SPIDER的架構與單發脈沖測量完全兼容[22]。2015年首次展示了單發d-scan[60]。下面，回顧了單發、基于SHG的d-scan裝置的發展進展，并討論了它們與掃描d-scan方法在少周期光脈沖和多周期光脈沖下的性能。

為了進行單發測量，應從光學裝置中消除所有移動元件。到目前為止，已經展示了如圖5所示的兩種完全不同的方法：首先，實現了一個光學元件，該元件將不同數量的GDD編碼到空間光束剖面的不同部分。其次，利用了一種特殊的非線性材料，同時引入了色散和非線性。這兩種方法的共同點是將色散軸轉換為空間方向。第1種方法z方便的實現方法是將標準d-scan中的掃描楔替換為棱鏡，該棱鏡在光束剖面上引入空間變化色散(圖5(a)中的SVD)。通過棱鏡后，光可能被聚焦成一條線，進入SHG晶體，此時沿著這條線的不同位置編碼對應不同色散量的SHG信號。如果用成像光譜儀對沿線的SHG信號進行成像，則可以在一次拍攝中獲得d-scan跡線。

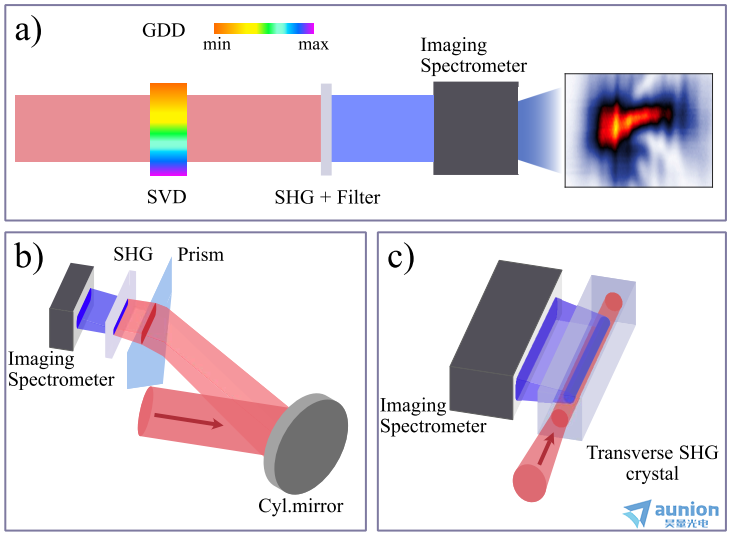
圖5所示。單次d-scan測量原理(a): SVD - SPA-初始可變色散。測量少周期(b)和多周期(c)脈沖的可能幾何形狀。

首次報道的這種設置被設計用于表征來自空芯光纖壓縮器的少周期脈沖[60]。在這個實驗中，用一條狹縫做成一條線，穿過BK7棱鏡。棱鏡的輸出面成像在薄BBO晶體上，這是必要的，以減輕不可避免地發生在棱鏡背面的角色散。雖然這種實現在概念上是直接的，但使用狹縫進行波束整形可能會限制所獲得的d-scan跡線的信噪比，并且裝置相當笨重。通過簡單地去除狹縫并使用全光束輪廓可以提高信噪比，但需要不同的聚焦幾何形狀。一個優雅的解決方案是讓光束先通過棱鏡，然后以較大的離軸角度反射到球面鏡上，產生強烈的散光。通過調整棱鏡、反射鏡和SHG晶體之間的角度和距離，可以在一個維度上聚焦光束，同時在另一個維度上將棱鏡的表面成像到晶體上，從而實現更緊湊、更節省空間的設計[61]。圖5(b)描述了一個類似但更簡單的配置，其中光束用圓柱形反射鏡聚焦到SHG晶體上的一條線上，而棱鏡置于兩者之間。鏡子上的入射角和棱鏡的旋轉必須仔細對準，以盡量減少像差。在這里，棱鏡的角啁啾不能通過對其輸出面進行成像來消除，但通過將SHG晶體直接放在棱鏡之后并盡可能靠近棱鏡，可以將其影響降到z低。由于光束在通過棱鏡的過程中受到聚焦，因此應注意避免棱鏡中的非線性效應。zui后，所有討論的實現的共同點是需要一個足夠均勻的光束輪廓-光束上顯著的強度變化會降低測量的精度。在實際操作中，可以在設置之前使用放大鏡和光圈來選擇光束輪廓的中心部分進行測量。

對于長脈沖的表征，上面討論的方法不再實用，因為在單個棱鏡中可以實現的相當大的光束尺寸的色散變化量(例如玻璃插入窗口)被限制在幾百fs2的GDD。圖5(c)描述了一種優雅的替代方案，它也非常適合于更長的脈沖。在這種實現中，一種高色散無序非線性晶體(硝酸鍶鋇，SBN)允許寬帶橫向二次諧波產生(TSHG)，同時用作色散和非線性元件[62]。隨機有序非線性晶體的特殊優點是其大色散，約為500 fs2/mm。初始負啁啾脈沖進入材料后逐漸壓縮，并垂直于傳播方向產生二次諧波。利用成像譜儀記錄了SHG，單次獲得了d-scan軌跡。對于典型的晶體長度為10 mm，獲得的總色散窗口為5000 fs2，允許在近紅外光譜范圍內測量持續時間長達60 fs的多周期脈沖[62]。

為了演示單發d-scan實現的性能，我們分別使用圖5(b)和(c)所示的幾何形狀，對基于HCF的后壓縮級后的近單周期脈沖和來自標準mJ級Ti:Sapphire CPA系統的多周期脈沖進行了表征。在這兩種情況下，SHG信號都是用自制的成像光譜儀檢測的，采用緊湊的交叉Czerny-Turner設計[63]，依靠光柵的發散照明來校正成像路徑的像散[64,65]。更多關于光譜儀設計的信息，如組件之間的距離和角度，可以在[61]中找到。在ccd傳感器前加一個圓柱透鏡[66]用于額外的像差校正。

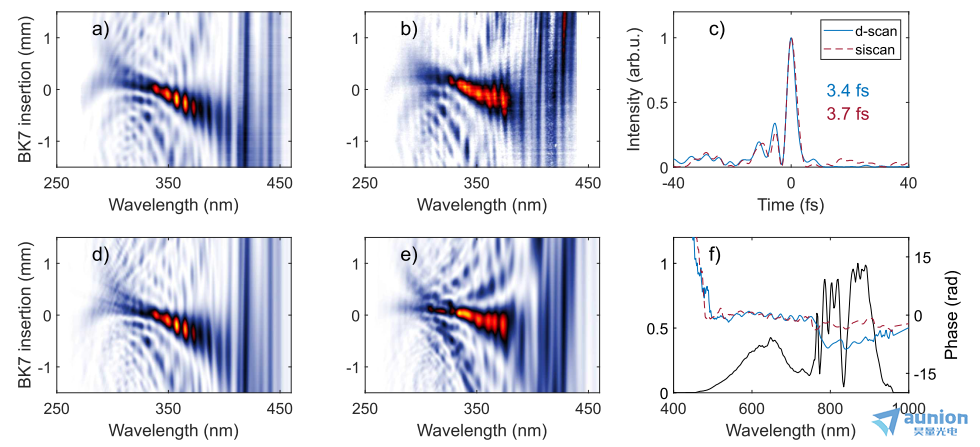
圖6所示。使用(a)標準裝置和(b)單發裝置對HCF壓縮器系統進行跡線測量，結果分別見(d)和(e)。(c)兩種方法反演到的脈沖強度分布圖，其中顯示了FWHM持續時間。(f)測得的光譜和反演到的光譜相位。藍線是通過掃描d-scan獲得的，而紅線對應于單發測量(siscan)。

圖6顯示了對少周期脈沖進行表征的結果。通過掃描(圖6(a))和單發(圖6(b))實現獲得的d-scan跡線是很一致的，正如反演到的脈沖持續時間分別為3.4 fs和3.7 fs所證實的那樣。兩個實驗都顯示出跡線的輕微傾斜，表明有少量未補償的三階色散，這也是反演強度分布圖中的預脈沖的特征(圖6(c))。掃描和單發測量的均方根誤差G分別為1.5%和7%。在頻域中，在波長λs= 766 nm之前，光譜相位一致，之后我們觀察到5.5 rad的相對位移幾乎恒定，這可以歸因于λs處的低光譜幅度，在局部引入了高度的相位值不確定性。然而，對時間剖面的一致性至關重要的不是相位本身，而是它的二階導數。因此，在反演相位中的恒定位移不對應于不同的脈沖。

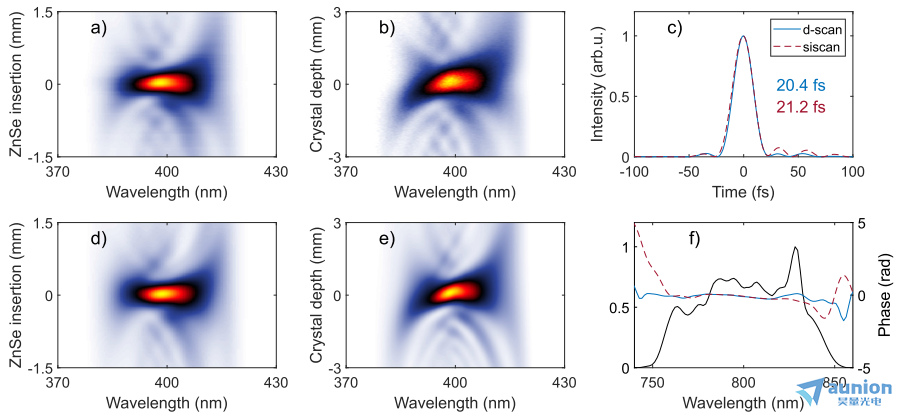
圖7所示。測量跡線(a)使用標準和(b)單發裝置的Ti:Sapphire CPA系統，反演結果分別顯示在(d)和(e)中。(c)兩種方法反演到的脈沖強度分布圖，其中顯示了FWHM持續時間。(f)測得的光譜和反演到的光譜相位。藍線是通過掃描d-scan獲得的，而紅線對應于單次測量(siscan)。

基于隨機非線性晶體(圖5(c))的實現結果總結在圖7中。測量使用1 kHz, mJ級，Ti:Sapphire CPA激光系統在LLC下進行，發射持續時間約為20 fs (FHWM)的近變換限制脈沖。如圖7(a)所示，傳統的(掃描)d-scan測量使用了一對硒化鋅楔形，在近紅外中具有極大的色散(GVD = 1025 fs2/mm)。聲光可編程色散濾波器(Dazzler, Fastlite)是CPA鏈的重要組成部分，引入了負啁啾。單發裝置使用10毫米長的SBN晶體，在800 nm處群速度色散為480 fs2/mm。結果如圖(b)所示。同樣，實驗軌跡非常一致，而寬度的差異可歸因于色散窗范圍的略微不同以及單次測量的殘余TOD量較大。脈沖反演結果在時間強度分布(圖7(c))和反演的光譜相位(圖7(d))方面在兩種設置之間非常吻合(掃描d-scan的RMS誤差為0.4%，單次掃描的RMS誤差為1.9%)。

5. 結論
本文綜述了利用二次諧波色散掃描技術表征脈沖特性的研究進展。我們表明，用d-scan獲得的跡線自然非常直觀地解釋，不同的多項式對脈沖光譜相位的貢獻表現為跡線的特征變形。本文還簡要介紹了可用于反演精確脈沖信息的相位重建算法。通過采用不同的脈沖壓縮器配置，d-scan可以成功地適應不同脈寬和中心頻率的脈沖測量。此外，我們提出了兩種不同的單發測量實現方案，非常適合于具有低重復率或大量脈沖對脈沖波動的脈沖源的表征，其中傳統的(掃描)d-scan要么花費不方便的長時間，要么導致誤導性的結論。

到目前為止，d-scan主要用于近紅外光譜范圍內脈沖的表征，這些脈沖來自Ti: Sapphire或摻Yb激光器，但對其他波長范圍的適應是直接的。近年來，在短波、中波和長波紅外光譜區以及深紫外提供超短脈沖的光源的開發方面取得了很大進展[67-72]。將d-scan技術擴展到不同的載波波長是一個正在進行的研究課題(參見UV范圍的例子[53])，毫無疑問，未來我們將在這個方向上看到更多的工作。

上海昊量光電作為Sphere Fast Photonics的中國代理，為您提供專業的選型以及技術服務。對于d-scan飛秒脈沖測量與壓縮器有興趣或者任何問題，都歡迎通過電話、電子郵件或者微信與我們聯系。

關于昊量光電：
上海昊量光電設備有限公司是光電產品專業代理商，產品包括各類激光器、光電調制器、光學測量設備、光學元件等，涉及應用涵蓋了材料加工、光通訊、生物醫療、科學研究、國防、量子光學、生物顯微、物聯傳感、激光制造等；可為客戶提供完整的設備安裝，培訓，硬件開發，軟件開發，系統集成等服務。

參考文獻：
1. W. E. Lamb, “Theory of an optical maser,” Phys. Rev. 134, A1429–A1450 (1964).
2. E.P. Ippen, C.V. Shank and A. Dienes, “Passive mode locking of the cw dye laser,” Appl. Phys. Lett. 21, 348–350 (1972).
3. P. F. Moulton, “Spectroscopic and laser characteristics of Ti:Al2O3,” J. Opt. Soc. Am. B 3, 125–133 (1986).
4. D. Strickland and G. Mourou, “Compression of amplified chirped optical pulses,” Opt. Commun. 56, 219 (1985).
5. D. E. Spence, P. N. Kean, and W. Sibbett, “60-fsec pulse generation from a self-mode-locked Ti:sapphire laser,” Opt. Lett. 16, 42 (1991).
6. R. L. Fork, C. H. B. Cruz, P. C. Becker, and C. V. Shank, “Compression of optical pulses to six femtoseconds by using cubic phase compensation,” Opt. Lett. 12, 483 (1987).
7. M. Nisoli, S. D. Silvestri, and O. Svelto, “Generation of high energy 10 fs pulses by a new pulse compression technique,” Appl. Phys. Lett. 68, 2793 (1996).
8. M. Nisoli, S. D. Silvestri, O. Svelto, R. Szipöcs, K. Ferencz, C. Spielmann, S. Sartania, and F. Krausz, “Compression of high-energy laser pulses below 5 fs,” Opt. Lett. 22, 522 (1997).
9. G. G. Paulus, F. Grasbon, H. Walther, P. Villoresi, M. Nisoli, S. Stagira, E. Priori, and S. De Silvestri, “Absolute-phase phenomena in photoionization with few-cycle laser pulses,” Nature 414, 182 (2001).
10. A. Schiffrin, T. Paasch-Colberg, N. Karpowicz, V. Apalkov, D. Gerster, S. Mühlbrandt, M. Korbman, J. Reichert, M. Schultze, S. Holzner, J. V. Barth, R. Kienberger, R. Ernstorfer, V. S. Yakovlev, M. I. Stockman, and F. Krausz, “Optical-field-induced current in dielectrics,” Nature 493, 70–74 (2013).
11. A. McPherson, G. Gibson, H. Jara, U. Johann, T. S. Luk, I. A. McIntyre, K. Boyer, and C. K. Rhodes, “Studies of multiphoton production of vacuum-ultraviolet radiation in the rare gases,” J. Opt. Soc. Am. B 4, 595 (1987).
12. M. Ferray, A. L’Huillier, X. Li, L. Lompre, G. Mainfray, and C. Manus, “Multiple-harmonic conversion of 1064 nm radiation in rare gases,” J. Phys. B 21, L31 (1988).
13. P.M. Paul, E.S. Toma, P. Breger, G. Mullot, F. Augé, Ph. Balcou, H.G. Muller, P. Agostini, “Observation of a Train of attosecond pulses from high harmonic Generation,” Science 292, 1689 (2001).
14. M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinz-mann, M. Drescher, and F. Krausz, “Attosecond metrology,” Nature 414, 509–513 (2001).
15. T. Gaumnitz, A. Jain, Y. Pertot, M. Huppert, I. Jordan, F. Ardana-Lamas, and H. J. Wörner, “Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver,” Opt. Express 25, 27506 (2017).
16. E. Goulielmakis, M. Uiberacker, R. Kienberger, A. Baltuska, V. Yakovlev, A. Scrinzi, T. Westerwalbesloh, U. Kleineberg, U. Heinzmann, M. Drescher, and F. Krausz, “Direct measurement of light waves,” Science 305, 1267–1269 (2004).
17. S. Keiber, S. Sederberg, A. Schwarz, M. Trubetskov, V. Pervak, F. Krausz, and N. Karpowicz, “Electro-optic sampling of near-infrared waveforms,” Nat. Photon. 10, 159–162 (2016).
18. E. P. Ippen and C. V. Shank, Ultrashort Light Pulses: Picosecond Techniques and Applications (Springer Berlin Heidelberg, 1977), chap. Techniques for Measurement, pp. 83–122.
19. J.-H. Chung and A. M. Weiner, “Ambiguity of ultrashort pulse shapes retrieved from the intensity auto-correlation and the power spectrum,” IEEE Journal of selected topics in quantum electronics 7, 656–666 (2001).
20. D. J. Kane and R. Trebino, “Characterization of Arbitrary femtosecond pulses Using Frequency-Resolved Optical Gating,” IEEE J. Quantum Electron. 29, 571 (1993).
21. R. Trebino and D. J. Kane, “Using phase retrieval to measure the intensity and phase of ultrashort pulses: frequency-resolved optical gating,” J. Opt. Soc. Am. A 10, 1101 (1993).
22. C. Iaconis and I. A. Walmsley, “Spectral phase interferometry for direct electric field reconstruction of ultrashort optical pulses,” Opt. Lett. 23, 792 (1998).
23. A. S. Wyatt, I. A. Walmsley, G. Stibenz, and G. Steinmeyer, “Sub-10 fs pulse characterization using spatially encoded arrangement for spectral phase interferometry for direct electric field reconstruction,” Opt. Lett. 31, 1914–1916 (2006).
24. V. V. Lozovoy, I. Pastirk, and M. Dantus, “Multiphoton intrapulse interference. IV. Ultrashort laser pulse spectral phase characterization and compensation,” Opt. Lett. 29, 775–777 (2004).
25. S. Grabielle, N. Forget, S. Coudreau, T. Oksenhendler, D. Kaplan, J.-F. Hergott, and O. Gobert, “Local Spectral Compression method for CPA lasers,” in CLEO/Europe and EQEC 2009 Conference Digest, (Optical Society of America, 2009), p. CF_P17.
26. V. Loriot, G. Gitzinger, and N. Forget, “Self-referenced characterization of femtosecond laser pulses by chirp scan,” Opt. Express 21, 24879–24893 (2013).
27. M. Miranda, T. Fordell, C. Arnold, A. L’Huillier, and H. Crespo, “Simultaneous compression and characterization of ultrashort laser pulses using chirped mirrors and glass wedges,” Opt. Express 20, 688–697(2012).
28. M. Miranda, C. L. Arnold, T. Fordell, F. Silva, B. Alonso, R. Weigand, A. L’Huillier, and H. Crespo, “Characterization of broadband few-cycle laser pulses with the d-scan technique,” Opt. Express 20, 18732–18743 (2012).
29. C. S. Gonçalves, A. S. Silva, D. Navas, M. Miranda, F. Silva, H. Crespo, and D. S. Schmool, “A dual-colour architecture for pump-probe spectroscopy of ultrafast magnetization dynamics in the sub-10-femtosecond range,” Sci. Reports 6, 22872– (2016).
30. C. Maibohm, F. Silva, E. Figueiras, P. T. Guerreiro, M. Brito, R. Romero, H. Crespo, and J. B. Nieder, “Syncrgb-flim: synchronous fluorescence imaging of red, green and blue dyes enabLED by ultra-broadband few-cycle laser excitation and fluorescence lifetime detection,” Biomed. Opt. Express 10, 1891–1904(2019).
31. A. Weiner, “Effect of group velocity mismatch on the measurement of ultrashort optical pulses via second harmonic generation,” IEEE J. Quantum. Electron. 19, 1276–1283 (1983).
32. A. Baltuska, M. S. Pshenichnikov, and D. A. Wiersma, “Second-harmonic generation frequency-resolved optical gating in the single-cycle regime,” IEEE J. Quantum Electron. 35, 459–478 (April 1999).
33. E. Conejero Jarque, J. San Roman, F. Silva, R. Romero, W. Holgado, M. A. Gonzalez-Galicia, B. Alonso,I. J. Sola, and H. Crespo, “Universal route to optimal few- to single-cycle pulse generation in hollow-core fiber compressors,” Sci. Reports 8, 2256– (2018).
34. F. Silva, B. Alonso, W. Holgado, R. Romero, J. S. Román, E. Conejero Jarque, H. Koop, V. Pervak, H. Crespo, and I. J. Sola, “Strategies for achieving intense single-cycle pulses with in-line post-compression setups,”Opt. Lett. 43, 337–340 (2018).
35. B. Alonso, I. Sola, and H. Crespo, “Self-calibrating d-scan: measuring ultrashort laser pulses on-target using an arbitrary pulse compressor,” Sci. Reports 8, 3264– (2018).
36. B. Alonso, S. Torres-Peiró, R. Romero, P. T. Guerreiro, A. Almagro-Ruiz, H. Muñoz Marco, P. Pérez-Millán, and H. Crespo, “Detection and elimination of pulse train instabilities in broadband fibre lasers using dispersion scan,” Sci. Reports 10, 7242– (2020).
37. E. Escoto, A. Tajalli, T. Nagy, and G. Steinmeyer, “Advanced phase retrieval for dispersion scan: a comparative study,” J. Opt. Soc. Am. B 35, 8–19 (2018).
38. A. Baltuska, A. Pugzlys, M. Pshenichnikov, and D. Wiersma, “Rapid amplitude-phase reconstruction of femtosecond pulses from intensity autocorrelation and spectrum,” in Technical Digest. Summaries of papers presented at the Conference on Lasers and Electro-Optics. Postconference Edition. CLEO ’99. Conference on Lasers and Electro-Optics (IEEE Cat. No.99CH37013), (1999), pp. 264 –265.
39. R. W. Gerchberg and W. O. Saxton, “A practical algorithm for the determination of phase from image and diffraction plane pictures,” Optik 35, 237–246 (1972).
40. D. J. Kane, “Real-Time Measurement of Ultrashort Laser Pulses Using Principal Component Generalized projections,” IEEE J. Sel. Top. Quantum Electron. 4, 278–284 (1998).
41. D. Kane, “Principal components generalized projections: a review,” J. Opt. Soc. Am. B 25, A120–A132 (2008).
42. N. C. Geib, M. Zilk, T. Pertsch, and F. Eilenberger, “Common pulse retrieval algorithm: a fast and universal method to retrieve ultrashort pulses,” Optica 6, 495–505 (2019).
43. D. E. Wilcox and J. P. Ogilvie, “Comparison of pulse compression methods using only a pulse shaper,” J.Opt. Soc. Am. B 31, 1544–1554 (2014).
44. M. Miranda, J. Penedones, C. Guo, A. Harth, M. Louisy, L. Neoriˇci´c, A. L’Huillier, and C. L. Arnold, “Fast iterative retrieval algorithm for ultrashort pulse characterization using dispersion scans,” J. Opt. Soc. Am. B 34, 190–197 (2017).

45. T. Zahavy, A. Dikopoltsev, D. Moss, G. I. Haham, O. Cohen, S. Mannor, and M. Segev, “Deep learning reconstruction of ultrashort pulses,” Optica 5, 666–673 (2018).

46. S. Kleinert, A. Tajalli, T. Nagy, and U. Morgner, “Rapid phase retrieval of ultrashort pulses from dispersion scan traces using deep neural networks,” Opt. Lett. 44, 979–982 (2019).

47. O. Pérez-Benito and R. Weigand, “Nano-dispersion-scan: measurement of sub-7-fs laser pulses using second-harmonic nanoparticles,” Opt. Lett. 44, 4921–4924 (2019).

48. F. Silva, M. Miranda, B. Alonso, J. Rauschenberger, V. Pervak, and H. Crespo, “Simultaneous compression, characterization and phase stabilization of GW-level 1.4 cycle VIS-NIR femtosecond pulses using a single dispersion-scan setup,” Opt. Express 22, 10181–10191 (2014).

49. M. Miranda, F. Silva, L. Neoriˇci´c, C. Guo, V. Pervak, M. Canhota, A. S. Silva, I. J. Sola, R. Romero, P. T. Guerreiro, A. L’Huillier, C. L. Arnold, and H. Crespo, “All-optical measurement of the complete waveform of OCTave-spanning ultrashort light pulses,” Opt. Lett. 44, 191–194 (2019).

50. F. Silva, M. Miranda, S. Teichmann, M. Baudisch, M. Massicotte, F. Koppens, J. Biegert, and H. Crespo, “Pulse measurement from near to mid-IR using third harmonic generation dispersion scan in multilayer graphene,” in 2013 Conference on Lasers and Electro-Optics - International Quantum Electronics Conference, (Optical Society of America, 2013), p. CFIE_3_5.

51. M. Hoffmann, T. Nagy, T. Willemsen, M. Jupé, D. Ristau, and U. Morgner, “Pulse characterization by THG d-scan in absorbing nonlinear media,” Opt. Express 22, 5234–5240 (2014).

52. A. Tajalli, B. Chanteau, M. Kretschmar, H. Kurz, D. Zuber, M. Kovaˇcev, U. Morgner, and T. Nagy, “Few-cycle optical pulse characterization via cross-polarized wave generation dispersion scan technique,” Opt. Lett.41, 5246–5249 (2016).

53. A. Tajalli, T. K. Kalousdian, M. Kretschmar, S. Kleinert, U. Morgner, and T. Nagy, “Full characterization of 8 fs deep uv pulses via a dispersion scan,” Opt.Lett 44, 2498–2501 (2019).

54. M. Canhota, F. Silva, R. Weigand, and H. M. Crespo, “Inline self-diffraction dispersion-scan of over octave-spanning pulses in the single-cycle regime,” Opt. Lett. 42, 3048–3051 (2017).

55. F. Böhle, M. Kretschmar, A. Jullien, M. Kovacs, M. Miranda, R. Romero, H. Crespo, U. Morgner, P. Simon, R. Lopez-Martens, and T. Nagy, “Compression of cep-stable multi-mj laser pulses down to 4fs in long hollow fibers,” Laser Phys. Lett. 11, 095401 (2014).

56. P. Rudawski, A. Harth, C. Guo, E. Lorek, M. Miranda, C. Heyl, E. Larsen, J. Ahrens, O. Prochnow, T. Bin-hammer, U. Morgner, J. Mauritsson, A. L’Huillier, and C. L. Arnold, “carrier-envelope phase dependent high-order harmonic generation with a high-repetition rate OPCPA-system,” Eur. Phys. J. D 69, 70 (2015).

57. A. Harth, C. Guo, Y.-C. Cheng, A. Losquin, M. Miranda, S. Mikaelsson, C. M. Heyl, O. Prochnow, J. Ahrens,U. Morgner, A. L’Huillier, and C. L. Arnold, “Compact 200 kHz HHG source driven by a few-cycle OPCPA,”J. Opt. 20, 014007 (2017).

58. A.-L. Viotti, B. Hessmo, S. Mikaelsson, C. Guo, C. Arnold, A. L’Huillier, B. Momgaudis, A. Melnikaitis, F. Laurell, and V. Pasiskevicius, “Soliton Self-Compression and Spectral Broadening of 1 µm Femtosecond Pulses in Single-Domain KTiOPO4 ,” in 2019 Conference on Lasers and Electro-Optics Europe and European Quantum Electronics Conference, (Optical Society of America, 2019), p. CF_4_5.

59. D. J. Kane and R. Trebino, “Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse by using frequency-resolved optical gating,” Opt. Lett. 18, 823 (1993).

60. D. Fabris, W. Holgado, F. Silva, T. Witting, J. W. G. Tisch, and H. Crespo, “Single-shot implementation of dispersion-scan for the characterization of ultrashort laser pulses,” Opt. Express 23, 32803–32808 (2015).

61. M. Louisy, C. Guo, L. Neoriˇci´c, S. Zhong, A. L’Huillier, C. L. Arnold, and M. Miranda, “Compact single-shot d-scan setup for the characterization of few-cycle laser pulses,” Appl. Opt. 56, 9084–9089 (2017).

62. F. J. Salgado-Remacha, B. Alonso, H. Crespo, C. Cojocaru, J. Trull, R. Romero, M. López-Ripa, P. T. Guerreiro, F. Silva, M. Miranda, A. L’Huillier, C. L. Arnold, and I. J. Sola, “Single-shot d-scan technique for ultrashort laser pulse characterization using transverse second-harmonic generation in random nonlinear crystals,” Opt. Lett. 45, 3925–3928 (2020).

63. M. Czerny and A. F. Turner, “Über den astigmatismus bei spiegelspektrometern,” Zeitschrift für Physik 61,792–797 (1930).

64. B. Bates, M. McDowell, and A. C. Newton, “Correction of astigmatism in a Czerny-Turner spectrograph using a plane grating in divergent illumination,” J. Phys. E: Sci. Instrum. 3, 206 (1970).

65. D. R. Austin, T. Witting, and I. A. Walmsley, “Broadband astigmatism-free Czerny-Turner imaging spectrometer using spherical mirrors,” Appl. Opt. 48, 3846–3853 (2009).

66. K.-S. Lee, K. P. Thompson, and J. P. Rolland, “Broadband astigmatism-corrected Czerny–Turner spectrometer,” Opt. Express 18, 23378–23384 (2010).

67. J. Li, X. Ren, Y. Yin, K. Zhao, A. Chew, Y. Cheng, E. Cunningham, Y. Wang, S. Hu, Y. Wu, M. Chini, and Z. Chang, “53-attosecond X-ray pulses reach the carbon K-edge,” Nat. Commun. 8, 186 (2017).

68. J. Pupeikis, P.-A. Chevreuil, N. Bigler, L. Gallmann, C. R. Phillips, and U. Keller,“Water window soft x-ray source enabled by a 25 W few-cycle 2.2 µm OPCPA at 100 kHz,” Optica 7, 168–171 (2020).

69. G. Andriukaitis, T. Balˇciunas, S. Ališauskas, A. Pugžlys, A. Baltuška, T. Popmintchev, M.-C. Chen, M. M.Murnane, and H. C. Kapteyn, “90 GW peak power few-cycle mid-infrared pulses from an optical parametric amplifier,” Opt. Lett. 36, 2755–2757 (2011).

70. M. Bock, L. von Grafenstein, U. Griebner, and T. Elsaesser, “Generation of millijoule few-cycle pulses at 5µm by indirect spectral shaping of the idler in an optical parametric chirped pulse amplifier,” J. Opt. Soc.Am. B 35, C18–C24 (2018).

71. F. Reiter, U. Graf, M. Schultze, W. Schweinberger, H. Schröder, N. Karpowicz, A. M. Azzeer, R. Kienberger,F. Krausz, and E. Goulielmakis, “Generation of sub-3 fs pulses in the deep ultraviolet,” Opt. Lett. 35,2248–2250 (2010).

72. M. Galli, V. Wanie, D. P. Lopes, E. P. Månsson, A. Trabattoni, L. Colaizzi, K.Saraswathula, A. Cartella,F. Frassetto, L. Poletto, F. Légaré, S. Stagira, M. Nisoli, R. Martínez Vázquez, R.Osellame, and F. Calegari,“Generation of deep ultraviolet sub-2-fs pulses,” Opt. Lett. 44, 1308–1311 (2019).